La récursivité…
La récursivité, c’est beau et pratique !

Qu’est-ce que la récursivité ?
Vu qu’on va parler de code, prenons la définition proposée par Wikipédia, à la page Algorithme récursif :
Un algorithme récursif est un algorithme qui résout un problème en calculant des solutions d’instances plus petites du même problème
En gros, c’est une fonction qui va s’appeler elle-même tant que le problème (qui est systématique le même…) à résoudre se présente.
Un exemple ?
Pour expliquer le principe, nous pouvons prendre l’exemple de gdf2bokeh, la librairie développée par mes soins, pour simplifier le traitement et l’affichage de données géographiques sur Bokeh (un article ici). Ces dernières sont constituées de géométries avec les types suivants :
- des points (Point) ;
- des lignes (LineString) ou groupes de lignes (MultiLineString) ;
- des polygones (Polygon) ou groupes de polygones (MultiPolygon) ;
- … et d’autres.
Nos géométries sont structurées sous la forme d’objet shapely, librairie dédiée au traitement géométrique, quasiment incontournable, pour manipuler ce type de données. Elle nous aidera à récupérer les coordonnées de nos objets.
Bokeh demande une structure de données assez précise qui requiert d’extraire et de stocker, séparemment, les coordonnées x et y de nos objets. Voici un exemple simple:
la LineString ou ligne qui a pour coordonnées (0, 2), (5, 2),(10, 10) devrait être transformée sous la forme de 2 listes : x = [0, 5, 10] y = [2, 2, 10]
Chaque type de géométrie possède des spécificités qui doivent être prises en charge, par exemple les trous dans les polygones, ou encore les MultiPart qui est une agglomération de plusieurs objets géométriques. Nous pouvons également rencontrer certains types, plus obscurs, tel que les LinearRing, lors du traitement des Polygones… A première vue, nous avons une diversité de structure. Néanmoins tous ces éléments ont un point commun: ils sont définis par 2 coordonnées géographiques (au moins). On peut même oser avancer la lapalissade suivante : tous nos objets géométriques ne sont finalement qu’une série de points… Seule leur organisation change selon le type.
Ainsi, la récursivité se prête donc très bien à notre problématique de conversion géométrique, car nos objets ont une cohérence qui s’articule sur un élément, une unité commune : le noeud (ou point).
Le code de la fonction récursive utilisé par gdf2Bokeh se trouve ici ; essayons de l’expliquer :
from typing import List
# Import de tous nos types de géométrie
from shapely.geometry import base
from shapely.geometry import Point
from shapely.geometry import MultiPoint
from shapely.geometry import LineString
from shapely.geometry import LinearRing
from shapely.geometry import MultiLineString
from shapely.geometry import Polygon
from shapely.geometry.polygon import InteriorRingSequence
from shapely.geometry import MultiPolygon
from shapely.geometry import GeometryCollection
from shapely.wkt import loads
def geometry_2_bokeh_format(geometry: base, coord_output_format: str = "xy") -> List:
"""
geometry_2_bokeh_format
To convert the geometry to display it with the bokeh library
:type geometry: shapely.geometry.*
:type coord_name: str, default: xy (x or y)
:return: float or list of tuple
"""
assert coord_output_format in ["xy", "x", "y"], f"coordinates output format {coord_output_format} not supported"
# la variable suivante va nous permettre de stocker nos coordonnées. Elle sera le résultat de cette méthode récursive.
coord_values: List = []
# nous enchaînons ensuite sur diverses conditions pour traiter chaque type géométrique. Chaque condition va affecter ou ajouter de nouvelles valeurs à la variable 'coord_values'.
# nous traitons ici le noeud (point), qui est notre plus petite unité et commune à tous les types de géométrie.
# cette condition sera la dernière appliquée à chacune de nos géométries.
if isinstance(geometry, Point):
# coord_values renvoie un tuple contenant un ou plusieurs flottant(s) liste de coordonnées x et/ou y
if coord_output_format != "xy":
coord_values = getattr(geometry, coord_output_format)
else:
coord_values = next(iter(geometry.coords))
# Le traitement des polygones en réutilisant la méthode
elif isinstance(geometry, Polygon):
# on traite le polygon extérieur (un LinearRing).
exterior = [geometry_2_bokeh_format(geometry.exterior, coord_output_format)]
# on traite les polygons intérieurs (des InteriorRingSequence.
interiors = geometry_2_bokeh_format(geometry.interiors, coord_output_format)
coord_values = [exterior, interiors]
if len(interiors) == 0:
coord_values = [exterior]
# Le traitement des LineString et LinearRing en réutilisant la méthode
elif isinstance(geometry, (LinearRing, LineString)):
coord_values = [
geometry_2_bokeh_format(Point(feat), coord_output_format)
for feat in geometry.coords
]
# Le traitement des MultiPolygon et MultiLineString en réutilisant la méthode
if isinstance(geometry, (MultiPolygon, MultiLineString)):
for feat in geometry.geoms:
# on va traiter ici soit des Polygons, soit des lignes
coord_values.extend(geometry_2_bokeh_format(feat, coord_output_format))
# le traitement des InteriorRingSequence en réutilisant la méthode
if isinstance(geometry, InteriorRingSequence):
coord_values.extend(
[geometry_2_bokeh_format(feat, coord_output_format) for feat in geometry]
)
if isinstance(geometry, (MultiPoint, GeometryCollection)):
raise ValueError(
f"no interest to handle {geometry.geom_type}"
)
# comme évoqué à l'entête de la méthode, on retourne la variable suivante, qui va s'alimenter progressivement grâce au rapel de la méthode dans chaque condition.
return coord_values
Voici également un schéma présentant le fonctionnement de cette méthode :
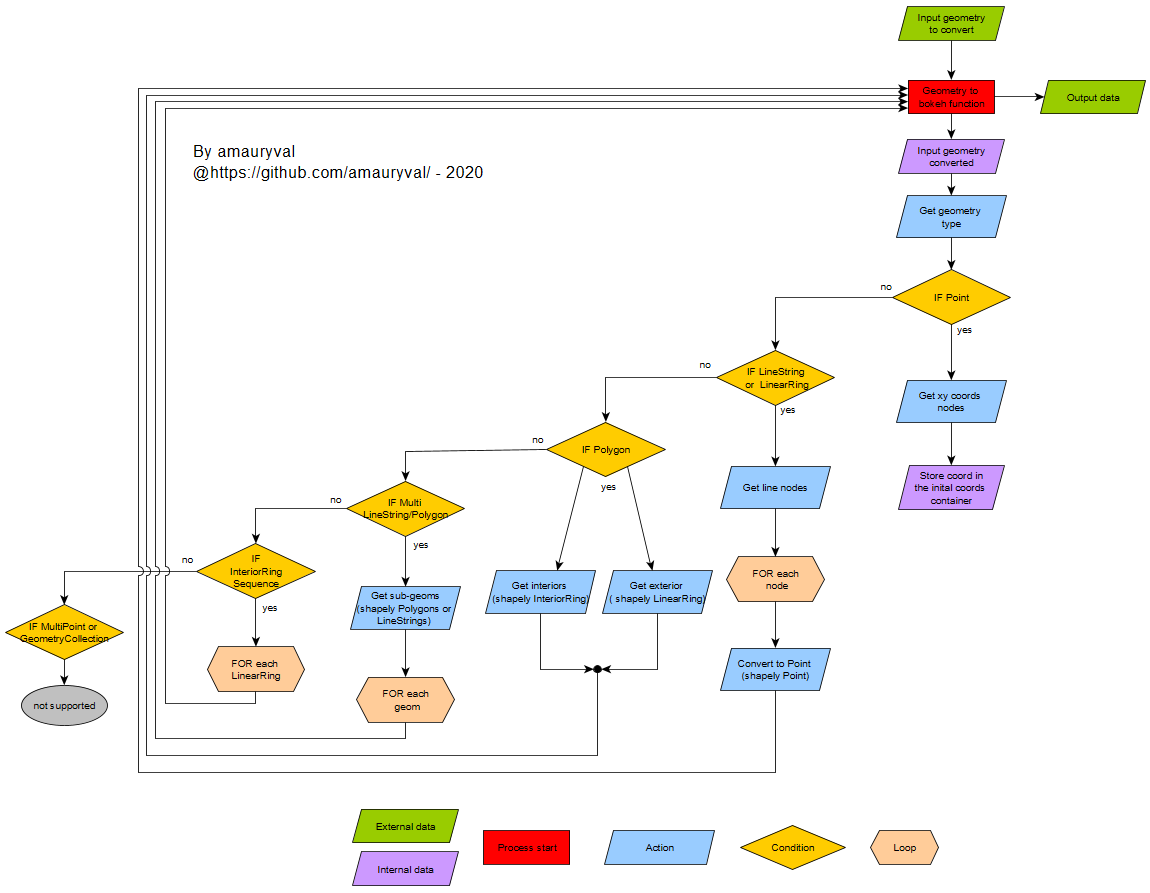
Sans ce mécanisme (qui peut paraître au premier abord tricky), le code aurait été plus long, redondant. On aurait peut-être eu autant de méthodes que de conditions pour gérer tous les cas, une lourdeur qui peut apporter de nombreuses confusions, au moment du débogage ou des mises à jour.
Voici quelques résultats:
from gdf2bokeh.helpers.geometry import geometry_2_bokeh_format
from shapely.geometry import Point
from shapely.geometry import LineString
from shapely.geometry import MultiLineString
from shapely.geometry import Polygon
point_xy_converted = geometry_2_bokeh_format(Point(0.0, 1.0), "xy")
# point_xy_converted output: (0.0, 1.0)
point_x_converted = geometry_2_bokeh_format(Point(0.0, 1.0), "x")
point_y_converted = geometry_2_bokeh_format(Point(0.0, 1.0), "y")
# point_x_converted output: 0.0
# point_y_converted output: 1.0
multilinestring_xy_converted = geometry_2_bokeh_format(MultiLineString([[(0, 0), (5, 2)], [(5, 2), (10, 10)]]), "xy")
# multilinestring_xy_converted output: [(0.0, 0.0), (5.0, 2.0)], [(5.0, 2.0), (10.0, 10.0)]
multilinestring_x_converted = geometry_2_bokeh_format(MultiLineString([[(0, 0), (5, 2)], [(5, 2), (10, 10)]]), "x")
multilinestring_y_converted = geometry_2_bokeh_format(MultiLineString([[(0, 0), (5, 2)], [(5, 2), (10, 10)]]), "y")
# multilinestring_x_converted output: [0.0, 5.0, 5.0, 10.0]
# multilinestring_y_converted output: [0.0, 2.0, 2.0, 10.0]
polygon_xy_converted = geometry_2_bokeh_format(Polygon([(0, 0), (1, 1), (1, 0), (0, 0)]), "xy")
# polygon_xy_converted output: [[[(0.0, 0.0), (1.0, 1.0), (1.0, 0.0), (0.0, 0.0)]]]
polygon_x_converted = geometry_2_bokeh_format(Polygon([(0, 0), (1, 1), (1, 0), (0, 0)]), "x")
polygon_y_converted = geometry_2_bokeh_format(Polygon([(0, 0), (1, 1), (1, 0), (0, 0)]), "y")
# polygon_x_converted output: [0.0, 1.0, 1.0, 0.0]
# polygon_y_converted output: [0.0, 1.0, 0.0, 0.0]
Comments